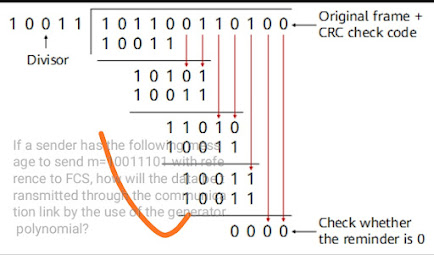
To transmit the message m=10011101 with reference to Frame Check Sequence (FCS) using a generator polynomial,
we need to perform a process called polynomial division. The generator polynomial is typically selected based on the specific communication protocol being used.
Assuming that the generator polynomial is G(x) = x^3 + x + 1 (which is a commonly used generator polynomial for communication protocols), we can perform the following steps:
1. Append the FCS bits to the message bits:
m = 10011101
FCS = 000
-----------------
data to be transmitted = 10011101000
2. Convert the message and FCS bits into a polynomial representation:
data(x) = x^9 + x^4 + x^3 + x^2 + 1
G(x) = x^3 + x + 1
3. Perform polynomial division of data(x) by G(x) using modulo-2 arithmetic:
x^6 + x^5 + x^3 + x^2
--------------------------
x^3 + x + 1 | x^9 + 0x^8 + 0x^7 + x^6 + 0x^5 + 0x^4 + x^3 + x^2 + 0x + 0
| x^9 + x^4 + x^3
----------------
x^5 + x^3 + x^2
x^5 + 0x^4 + x^3
--------------
x^4 + x^2
x^4 + 0x^3 + x^2
--------------
x^3 + x^2
x^3 + 0x^2 + x
------------
x^2 + x
x^2 + 0x + x
-----------
0
4. The result of the division is the quotient Q(x) = x^6 + x^5 + x^3 + x^2 and the remainder R(x) = 0. The transmitted message consists of the original message plus the FCS bits, which is 10011101000, where the last three bits are the FCS bits.
Therefore, the transmitted message with reference to FCS using the generator polynomial G(x) = x^3 + x + 1 is 10011101000.